Overview
For this project, my team and I were tasked with performing numerical analysis on a problem of our choice,incorporating real-world data. We implemented the Least Mean Squares (LMS) algorithm to reduce noise amplitude in sound samples collected from various campus locations. The algorithm was designed to selectively filter background noise while preserving critical emergency sounds.
Algorithm Selection
We initially explored Destructive Interference, a common Active Noise Cancellation (ANC) method used in noise-canceling headphones. This approach relies on combining two waves of the same amplitude but opposite phase to cancel each other out. To demonstrate its effectiveness, we created a MATLAB script that completely canceled a noise wave by inverting its phase. While this method effectively eliminates noise, its limitations for real-time noise cancellation and lack of safety by blocking out certain sounds led us to explore alternative algorithms.
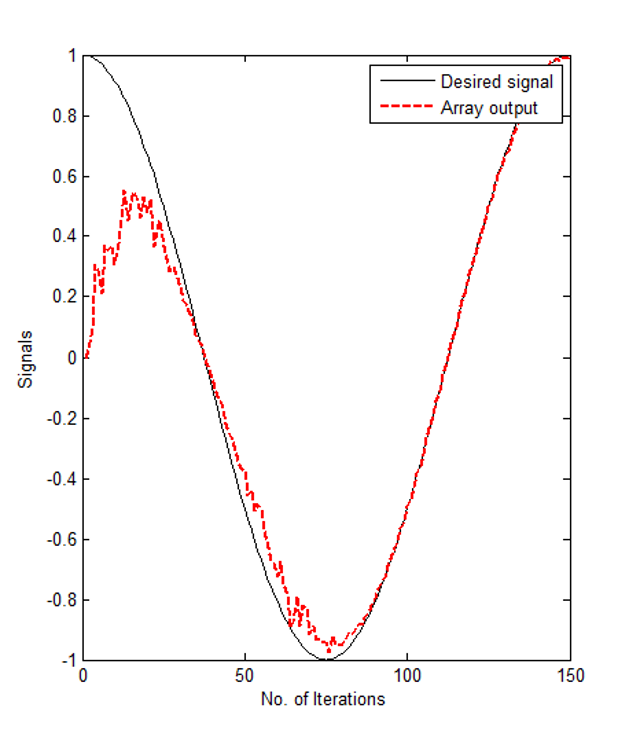
To address the limitations of Destructive Interference, we implemented the Least Mean Squares (LMS) algorithm. The LMS algorithm adapts dynamically to changes in the input signal, eliminating the need for real-time inversion of sound waves. Instead, it uses the steepest descent statistical analysis technique to iteratively update the coefficients of a digital filter. This minimizes the error between the output signal and the desired reference, enabling the LMS algorithm to "learn" and continuously improve its noise-filtering effectiveness over time.
MATLAB Code
To implement our noise cancellation algorithm, we developed a MATLAB script that processes an audio file by converting it to mono-channel format, since the algorithm only supports single-channel audio. The script generates white noise with an amplitude matching the average amplitude of the original audio. The desired clean signal is obtained by subtracting the noise from the original audio. The LMS algorithm is then applied, where the filter’s complexity is determined by the filter length, and the step size influences the rate of convergence and stability. The code enables us to compare the original and cleaned signals both visually, through plotting the signals, and audibly, by playing the audio files.
Analysis Process
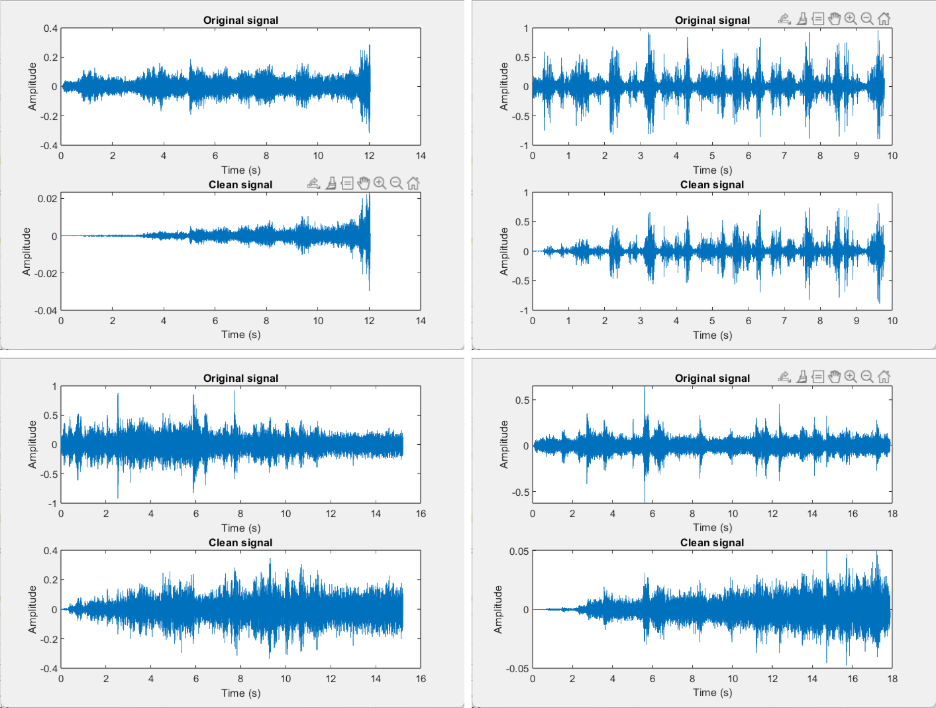
We collected noise samples from various high-traffic locations on campus, such as the gym, the lawn, buses, and study spots. We then ran our MATLAB code on these samples, generating graphs of the original and cleaned audio signals. Finally, we were able to evaluate the effectiveness of our algorithm by measuring the reduction in noise amplitude, as well as by listening to our audio files.
Results
My team and I found that our algorithm was capable of reducing sound by up to 95%, while still allowing emergency signals to be heard. Through this project, I gained hands-on experience with MATLAB scripting. I was also able to deepen my understanding of various algorithms and statistical techniques.
